Khối đa diện lớp 12: Công thức, lý thuyết và bài tập

Khối đa diện lớp 12 chiếm khá nhiều câu hỏi vận dụng cao trong đề thi toán THPT Quốc Gia. Vì vậy, việc nắm vững các dạng bài tập về khối đa diện lớp 12 là vô cùng quan trọng đối với các bạn học sinh. Trong bài viết dưới đây, BTEC FPT đã tổng hợp lại kiến thức trọng tâm, các công thức và kinh nghiệm làm bài tập khối đa diện lớp 12 cho các bạn học sinh tham khảo.

Khối đa diện là gì
Khối đa diện là gì
Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
- Hai đa giác bất kỳ hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
- Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Lý thuyết Khối đa diện lớp 12
1. Phân loại khối đa diện
Có hai loại khối đa diện:
👉 Xem thêm: Đề thi THPT Quốc Gia 2024 Môn Toán mới nhất
👉 Xem thêm: Bộ 20 đề thi thử THPT quốc gia 2024 môn toán (Có Lời Giải)
👉 Xem thêm: Tài liệu ôn thi THPT quốc gia 2024 môn toán
👉 Xem thêm: Bộ đề thi tham khảo THPT quốc gia 2024 môn toán
👉 Xem thêm: Cấu trúc đề thi thpt quốc gia môn toán 2024
👉 Xem thêm: Tổng hợp công thức toán thi thpt quốc gia mới nhất
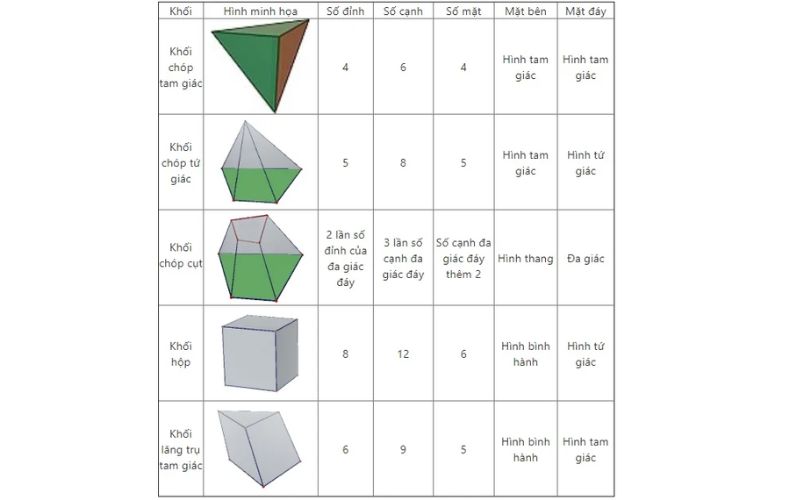
Khối đa diện lồi
- Khối đa diện lồi: Khối đa diện được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của luôn thuộc. Khi đó đa diện xác định được gọi là đa diện lồi.
- Khối đa diện đều là khối hình lồi có tính chất sau đây:
- Mỗi mặt của nó là một đa giác đều p cạnh.
- Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
- Khối đều như vậy được gọi là khối đa diện đều loại {p ; q}.
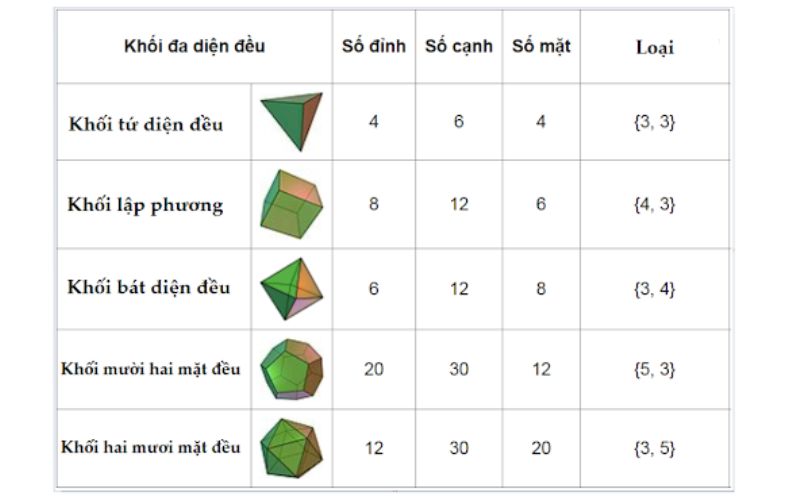
Khối đa diện đều
Từ định nghĩa trên ta thấy các mặt của khối đều là những đa giác đều bằng nhau
- Các loại khối đa diện đều phổ biến:
- Tứ giác đều
- Hình lập phương
- Bát diện đều
- Mười hai mặt đều
- Hai mươi mặt đều
Ví dụ:
- Khối lập phương: là một khối đa diện lồi có 6 mặt hình vuông.
- Tứ diện: là một khối đa diện lồi có 4 mặt hình tam giác.
- Hình chóp cụt: là một khối đa diện lõm có 2 mặt đáy hình đa giác và các mặt bên hình thang.
2. Tính chất của khối đa diện
- Số mặt: Số mặt của một khối đa diện bằng tổng số cạnh của nó trừ đi số đỉnh của nó cộng thêm 2.
- Số cạnh: Số cạnh của một khối đa diện bằng tổng số cạnh của các mặt của nó.
- Số đỉnh: Số đỉnh của một khối đa diện bằng số điểm chung của các cạnh của nó.
Đăng ký nhận học bổng ngay

3. Các dạng bài tập khối đa diện
Dưới đây là một số dạng bài tập thường gặp về khối đa diện:
Dạng 1: Xác định loại khối đa diện:
- Cho một hình đa diện, xác định loại khối đa diện đó (lăng trụ, chóp, hình hộp chữ nhật, tứ diện,...).
- Dựa vào các đặc điểm của hình đa diện (số mặt, số cạnh, số đỉnh,...), xác định loại khối đa diện đó.
Dạng 2: Tính số cạnh, số mặt, số đỉnh của khối đa diện:
- Cho một hình đa diện, tính số cạnh, số mặt, số đỉnh của hình đa diện đó.
- Sử dụng các công thức liên hệ giữa số cạnh, số mặt, số đỉnh của khối đa diện.
Dạng 3: Tính diện tích và thể tích của khối đa diện:
- Cho một hình đa diện, tính diện tích toàn phần, diện tích xung quanh và thể tích của hình đa diện đó.
- Sử dụng các công thức tính diện tích và thể tích của các loại khối đa diện thường gặp.
Dạng 4: Phân chia và lắp ghép khối đa diện:
- Chia một khối đa diện cho trước thành các khối đa diện nhỏ hơn.
- Lắp ghép các khối đa diện nhỏ hơn thành một khối đa diện cho trước.
Dạng 5: Chứng minh:
- Chứng minh các tính chất của khối đa diện.
- Chứng minh hai khối đa diện bằng nhau.

Các công thức giải Khối đa diện 12
Công thức chung để tính thể tích của một khối đa diện là:
V = 1/3 * S * h
Trong đó:
- V là thể tích của khối đa diện.
- S là diện tích đáy của khối đa diện.
- h là chiều cao của khối đa diện.
Công thức thể tích một số khối đa diện thường gặp:
- Khối lập phương: V = a^3 (a là độ dài cạnh)
- Hình hộp chữ nhật: V = abc (a, b, c là độ dài ba cạnh)
- Lăng trụ: V = S * h (S là diện tích đáy, h là chiều cao)
- Chóp: V = 1/3 * S * h (S là diện tích đáy, h là chiều cao)
- Hình cầu: V = 4/3 * π * r^3 (r là bán kính)
Lưu ý:
Các công thức trên chỉ áp dụng cho các khối đa diện lồi.
Đối với các khối đa diện lõm, cần chia khối đa diện thành các khối đa diện lồi và tính tổng thể tích của các khối đa diện lồi đó.
Kinh nghiệm làm bài tập Khối đa diện lớp 12
1. Nắm chắc lý thuyết
Trước hết, các bạn học sinh cần nắm chắc lý thuyết khối đa diện bao gồm khái niệm, phân loại, các công thức tính thể tích khối đa diện để có thể áp dụng vào giải bài tập. Để ghi nhớ kiến thức nhanh chóng, hiệu quả các bạn học sinh nên tự xây dựng cho mình sơ đồ tư duy cá nhân cho mỗi bài học.
Để giải đúng kết quả, việc vẽ hình chính xác là vô cùng quan trọng cần các bạn nắm vững các tính chất hình học khối đa diện và hình vẽ khối đa diện.
2. Luyện tập thường xuyên
Các bạn học sinh nên làm nhiều dạng bài tập khác nhau, bao gồm cả bài tập trắc nghiệm và bài tập tự luận có mức độ từ dễ đến khó. Việc luyện tập thường xuyên giúp các bạn làm quen với các dạng câu hỏi và phương pháp giải, từ đó nâng cao kỹ năng và điểm số.
Bên cạnh đó, các bạn học sinh cần chú ý chọn những nguồn tài liệu tham khảo uy tín, bám sát đề thi THPT Quốc Gia. Có rất nhiều nguồn tài liệu uy tín các bạn có thể tham khảo để luyện giải bài tập như sách giáo khoa, sách bài tập và các loại sách tham khảo được xuất bản bởi Bộ giáo dục và đào tạo, Đại học Quốc Gia Hà Nội,…
Bài tập khối đa diện lớp 12
👉 Xem thêm: Khối đa diện lớp 12: Công thức, lý thuyết và bài tập

Kinh nghiệm làm bài tập Khối đa diện lớp 12
Hy vọng với những kinh nghiệm mà chúng mình đã chia sẻ trên đây sẽ giúp các bạn học sinh có quá trình học tập và ôn thi hiệu quả khối đa diện lớp 12. BTEC FPT chúc bạn thành công trên con đường học tập.
Tin tức mới nhất
Nhập học liền tay










